Ableitung und Stammfunktion- Grafisch
Aufgabe 1:
Lösung:
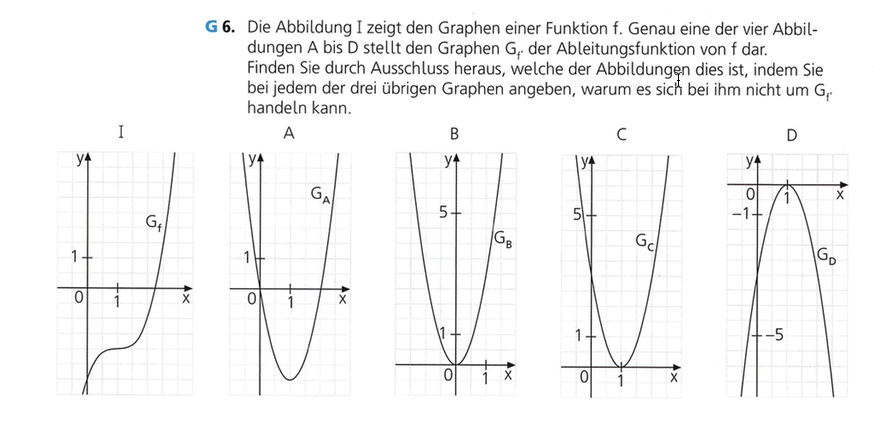
Zwei Kriterien genügen, um die Ableitung des Grafen (I) zu finden:
- (I) ist monoton steigend, d.h. \(f'(x) \ge 0\,\,\forall \,\,x\in {\mathbb{D}_f}\)
(I) besitzt genau eine Stelle mit waagrechter Tangente bei \(x=1\), d.h. \(f'(x)\) besitzt genau eine Nullstelle.
Damit erhält man:
A scheidet aus (Zwei Nullstellen)
D scheidet aus (\(f'(x) \le 0\,\,\forall \,\,x\in {\mathbb{D}_f}\))
Da die Stelle \(x=1\) keine Nullstelle von B ist, sondern \(x=0\), scheidet auch diese Möglichkeit aus.
Übrig bleibt also C.
Aufgabe 2:
Lösung:
Zunächst mal das Tafelbild im Original, dann die Erklärungen zum Vorwissen:
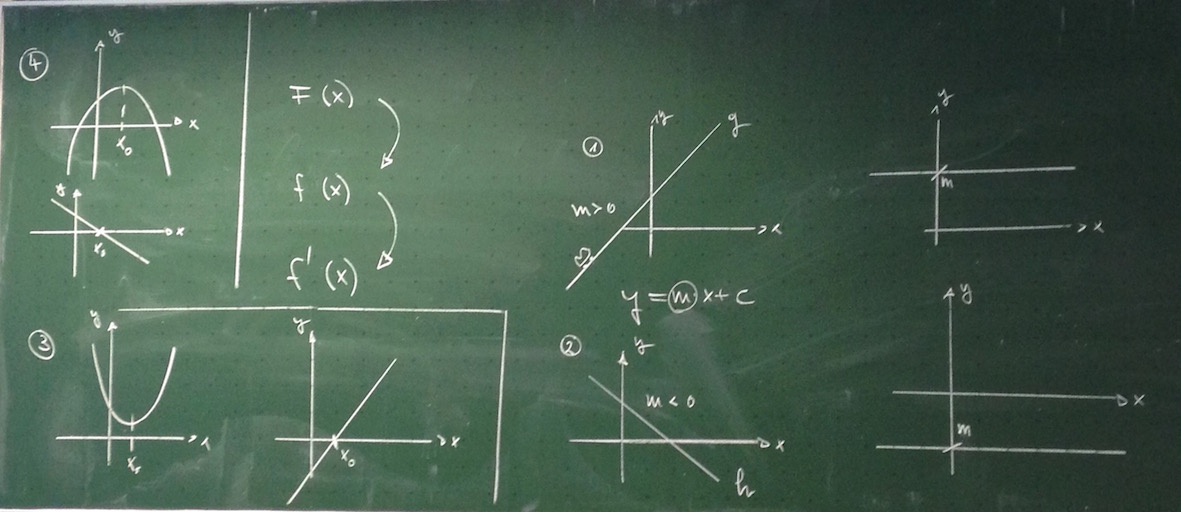
Im Einzelnen:
Jede Parabel \(y = a{x^2} + bx + c\) besitzt als Ableitungsfunktin die Gerade \(y = 2ax + b\). Für \(a>0\) steigt diese Gerade, für \(a<0\) fällt sie.
Zu einer nach oben geöffnete Parabel gehört also eine Gerade mit positiver Steigung als Graf der Ableitungsfunktion, zu einer nach unten geöffneten Parabel gehört eine Gerade mit negativer Steigung.
Die Ableitungungsfunktion einer Geraden \(y=mx+c\) ist die konstante Funktion \(y=m\). Deren Graf ist eine Parallele zur x - Achse! Für \(m>0\) oberhalb der x - Achse, für \(m<0\) unterhalb der x - Achse.
Für \(m=0\) hat man übrigens keine Geradengleichung, sondern nur die konstante Funktion \(y=c\). Deren Ableitungsfunktion ist \(y=0\). Konstanten haben die Ableitung Null und Graf dieser Ableitung ist die x - Achse selber (oder eine Gerade mit der Steigung 0).
Mit diesem Wissen lassen sich die Aufgaben leicht lösen:
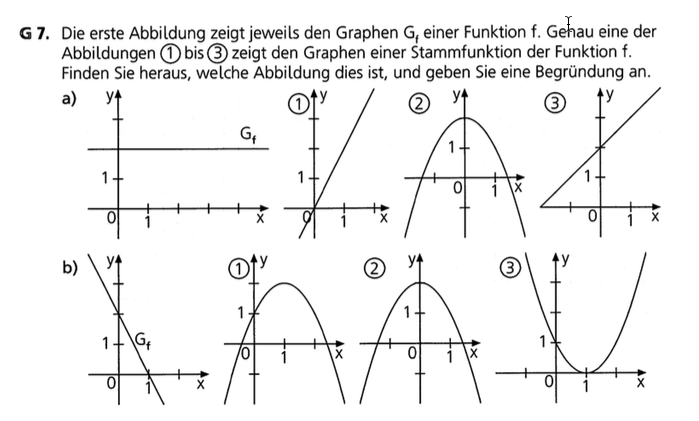
a) zeigt eine zur x - Achse parallele Gerade; der Graf deren Stammfunktion muss eine Gerade mit \(m\ne 0\) sein. Möglichkeit 2 scheidet also aus.
Da die Parallele oberhalb der x- Achse durch den Punkt \(P(0/2)\) verläuft, folgt \(m=2\) und Möglichkeit 1 als richtige Lösung. Möglichkeit 3 scheidet aus wegen der falschen Geradensteigung \(m=1\).
b) zeigt eine Gerade mit negativer Steigung. Der Graf einer Stammfunktion muss also eine nach unten geöffnete Parabel darstellen. Möglichkeit 3 scheidet also aus. Der Scheitelpunkt der Parabel besitzt eine waagrechte Tangente; diese Stelle muss gleichzeitig eine Nullstelle der Geraden sein. Die Gerade hat bei \(x=1\) eine Nullstelle und man erhält Möglichkeit 1 als richtige Lösung.